La paralaje
Para calcular la distancia de un planeta se puede utilizar la paralaje.
La paralaje consiste en poner un dedo ante los ojos. El fondo no debe ser uniforme. Sin mover la cabeza ni el dedo y mirando primero con un ojo y luego con otro, se puede ver que la posición del dedo respecto al fondo cambia. Si acercamos más el dedo a los ojos y volvemos a mirar primero con un ojo y luego con el otro, las dos posiciones del dedo contra el fondo abarcarán un parte mayor.
Esto es debido a que entre los dos ojos hay una separación de varios centímetros, así que la línea imaginaria que une el dedo con uno de los ojos forma un ángulo con la línea imaginaria que une el dedo con el otro ojo. Si prolongamos esas dos líneas imaginarias hasta el fondo, tendremos dos puntos que corresponderían a las dos posiciones aparentes del dedo.
Cuanto más cerca de los ojos pongamos el dedo, mayor será el ángulo y mayor también el desplazamiento aparente.
Si los ojos estuviesen más separados, aumentaría más el ángulo formado por las dos líneas, y así sería mayor el desplazamiento aparente del dedo contra el fondo.

Esto puede aplicarse también a un planeta. Es verdad que la Luna está tan lejos que no podremos notar ninguna diferencia cuando miremos con ambos ojos. Pero si miramos la Luna contra el fondo estrellado del cielo, desde dos observatorios alejados entre sí algunos cientos de kilómetros, sí notaremos algo. Desde el primer observatorio veremos que uno de los bordes de la Luna está a cierta distancia de una estrella concreta, mientras que en el segundo observatorio la distancia entre el mismo borde y la misma estrella será distinta.
Sabiendo el desplazamiento aparente de la Luna contra el fondo estrellado y la distancia entre ambos observatorios, puede calcularse la distancia ayudados por la trigonometría.
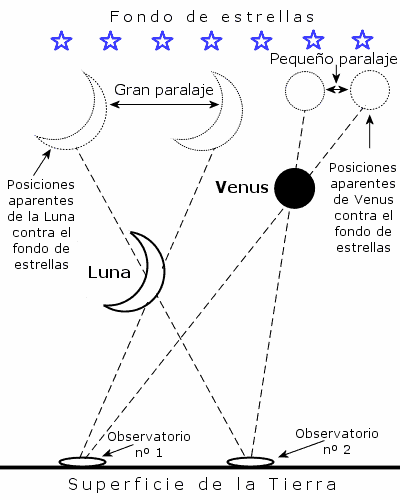
Este experimento podía hacerse perfectamente, porque el desplazamiento aparente de la Luna respecto al fondo estrellado al cambiar la posición del observador es muy grande. Los astrónomos han normalizado este desplazamiento para el caso de que uno de los observadores esté viendo la Luna en el horizonte y el otro justo sobre su cabeza. La base del triángulo será entonces igual al radio de la Tierra y el ángulo con vértice en la Luna es el «paralaje horizontal ecuatorial». Su valor es de 57,04 minutos de arco, o bien 0,95 grados de arco. Un desplazamiento apreciable realmente, porque equivale a dos veces el diámetro aparente de la Luna llena. Se trata de una magnitud que puede medirse con bastante precisión, y permite conseguir un buen valor para la distancia de la Luna. Esta distancia, calculada con ayuda de la paralaje, concuerda muy bien con la cifra obtenida por ese antiguo método basado en la sombra proyectada por la Tierra durante un eclipse lunar.
Desgraciadamente, las condiciones en el año 1600 no permitían colocar los observatorios a una suficiente distancia, lo cual, unido a la enorme distancia a la que se encuentran los planetas, hacía que el desplazamiento aparente contra el fondo estrellado fuese demasiado pequeño para poder ser medido de forma precisa.
Podemos decir que hay dos tipos de paralaje:
- Paralaje geocéntrica: cuando el radio utilizado es el terrestre.
- Paraleje helicéntrica o anual: cuando el radio utilizado es la órbita terrestre alrededor del Sol.
Si observamos una estrella en enero y en junio, en esos momentos la Tierra se encontrará en dos lugares opuestos de la órbita terrestre. Podemos medir el cambio de posición aparente de la estrella. Cuanta mayor sea la parelaje, más cerca estará esa estrella. Para ello se utiliza el parsec como unidad, y se define como la inversa de la paralaje trigonométrica medida en segundos de arco.
Más tarde, llegó el telescopio, inventado o reinventado por el científico italiano Galileo Galilei. El telescopio permitió que una distancia angular no detectable a simple vista pudiera medirse fácilmente.
Los planetas con paralajes mayores son los más cercanos, o sea, Marte y Venus. Venus, en su máximo acercamiento al Sol pasa tan cerca de él que resulta imposible observarlo, excepto en los tránsitos, en que puede verse contra el fondo del disco solar. Así que, el único caso para medir la paralaje era el planeta Marte.
La primera medida telescópica de una paralaje planetaria fue realizada en 1671. Los dos observadores eran Jean Richer, astrónomo francés, al frente de una expedición científica a Cayena, en Guayana Francesa y el astrónomo italo-francés Giovanni Cassini, que se quedó en París. Observaron Marte con la máxima simultaneidad posible y tomaron nota de su posición respecto a las estrellas más próximas. Calculada la diferencia de posiciones observada y conocida la distancia de Cayena a París, se calculó la distancia de Marte en el momento de la medición.
Una vez hecho esto, se tenía ya la escala del modelo de Kepler, lo que permitiría calcular todas las otras distancias del sistema solar. Cassini estimó que la distancia entre el Sol y la Tierra era de 140.000.000 de kilómetros, nueve millones de kilómetros por debajo de la cifra real, pero un excelente resultado para el primer intento.
Más tarde se realizaron mediciones algo más exactas de las paralajes planetarias. Algunas sobre Venus, en las ocasiones que pasa justo entre la Tierra y el Sol, y que puede verse como un pequeño círculo oscuro cruzando el disco del Sol. Estos tránsitos tuvieron lugar en 1761 y 1769. Si el tránsito se observa desde dos observatorios distintos, se puede comprobar que el momento en que Venus entra en contacto con el disco solar y también el momento en que se separa de él, que es el tiempo que dura el tránsito, varía de un observatorio a otro. Conocidas estas variaciones y las distancias entre los dos observatorios, se puede calcular la paralaje de Venus. Teniendo este dato, se puede calcular la distancia a Venus, y luego la distancia al Sol.
El astrónomo alemán Johann Franz Encke, en 1835, usó los datos existentes de los tránsitos de Venus para calcular la distancia del Sol, y la cifra fue de 153.450.000 de kilómetros. Excedía un poco de la cifra real, pero sólo en unos 3.000.000 de kilómetros.
Para conseguir valores más exactos la principal dificultad era que Venus y Marte eran vistos por el telescopio como diminutas esferas, lo que impedía fijar con precisión la posición del planeta. Especialmente decepcionante era Venus, porque la espesa capa atmosférica que posee producía efectos ópticos que impedían ver durante el tránsito el momento exacto del contacto con el disco solar.
De repente un inesperado acontecimiento sucedió. El astrónomo italiano Giuseppe Piazzi, en 1801, descubrió un pequeño cuerpo celeste cuya órbita se encontraba entre Marte y Júpiter, y lo llamó Ceres. Tenía un diámetro algo menor a 800 kilómetros. Conforme avanzó el siglo, se descubrieron cientos de planetas aún más pequeños, todos entre las órbitas de Marte y Júpiter. Eran los asteroides. Algo después, en 1898, Karl Gustav Witt, astrónomo alemán, descubrió Eros, un asteroide alejado de la zona de los asteroides. Una parte de su órbita pasaba por la de Marte, y muy cerca de la Tierra también.
Se calculó que en 1931 Eros se acercaría a la Tierra. Era una buena oportunidad para calcular la paralaje. Como Eros es muy pequeño, se calcula que su diámetro máximo es de 24 kilómetros, y no tiene atmósfera que pudiera difuminar su contorno, se observaría como un punto luminoso y podría calcularse bien su posición.
Se organizó un gran proyecto a escala internacional. Se tomaron y estudiaron miles de fotografías, y se llegó a la conclusión, a partir de la paralaje y de la posición de Eros, que el Sol se encuentra a algo menos de 150.000.000 de kilómetros de la Tierra. Esto es un promedio, pues la Tierra describe una elipse alrededor del Sol, no una circunferencia. El perihelio, o distancia mínima entre la Tierra y el Sol, es 147.000.000 de kilómetros y el afelio, máxima distancia de 152.200.000 de kilómetros.



